Interactive Ising Model Simulation
Access the online simulation here. View this project on GitHub here.
Model
The Ising Model is a nearest-neighbor numerical model for ferromagnetic behavior of atomic dipole lattice systems. This model assumes that atomic dipoles occupy only one of two anti-parallel states, which is modeled as quantized magnetization values of either +1 or -1 for each lattice unit.
Every turn, the algorithm iterates through every dipole and considers the projected change in total energy if each individual dipole were to be flipped. If flipping a dipole would result in a lower total energy, then it is always flipped. Otherwise, it is flipped randomly according to temperature and current-energy-state dependent Boltzmann statistics. The total energy is modeled using only the interactions of nearest cardinal neighbors. Learn more about the Ising Model here.
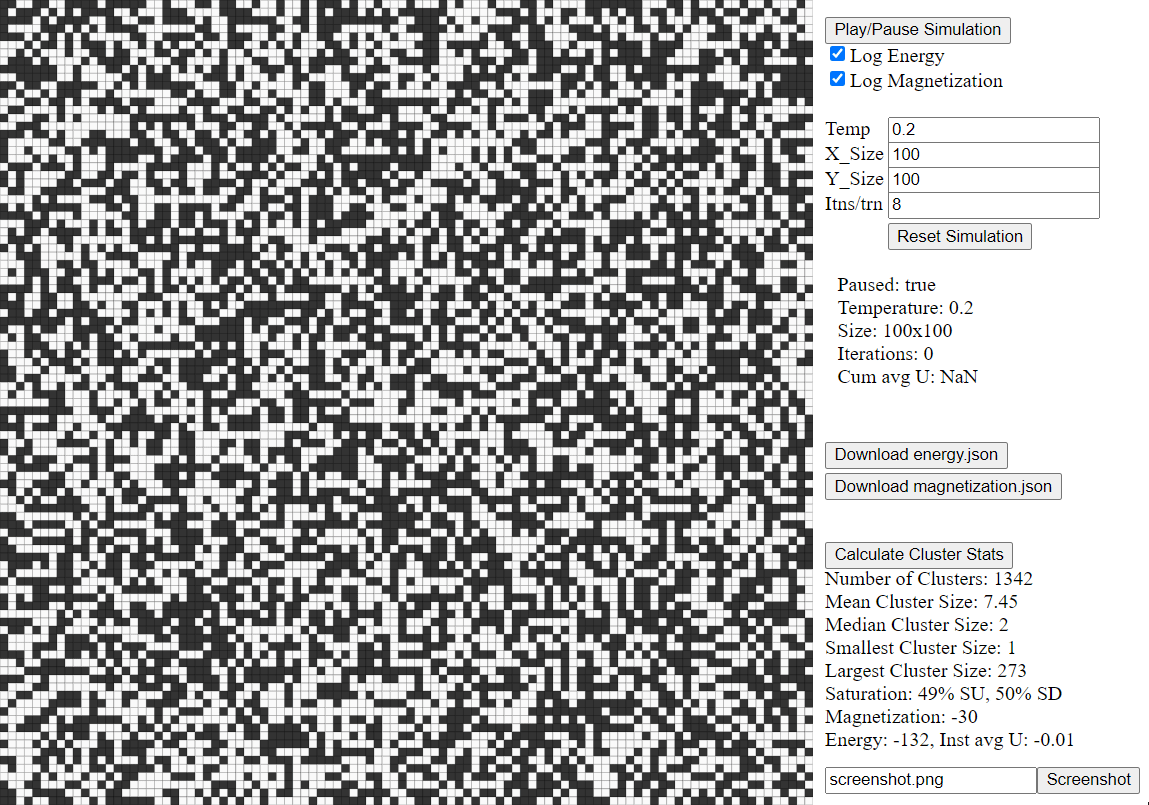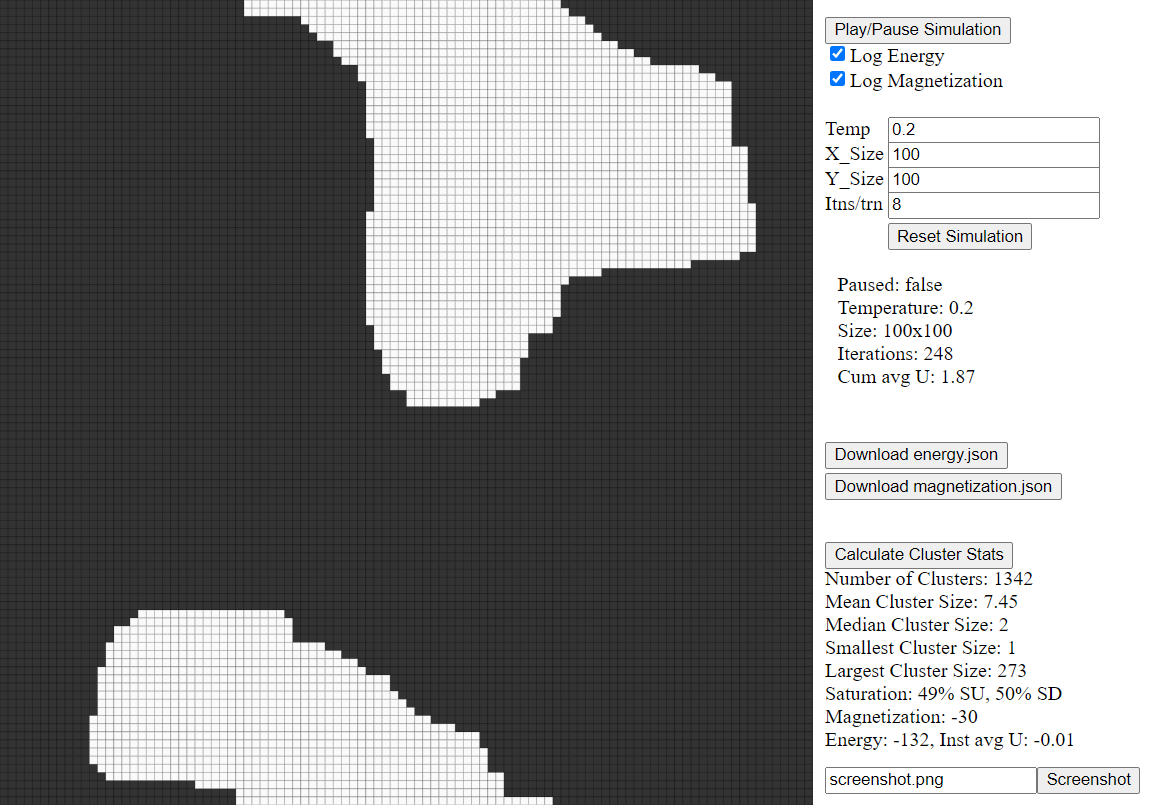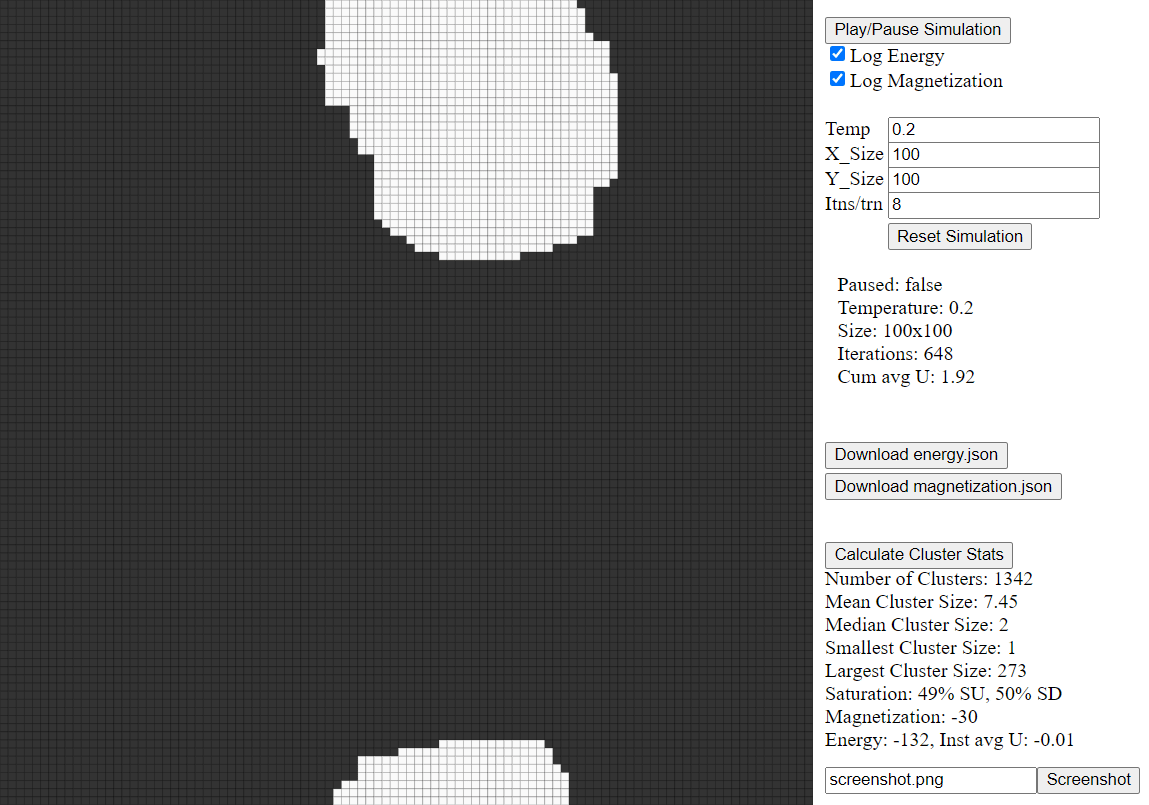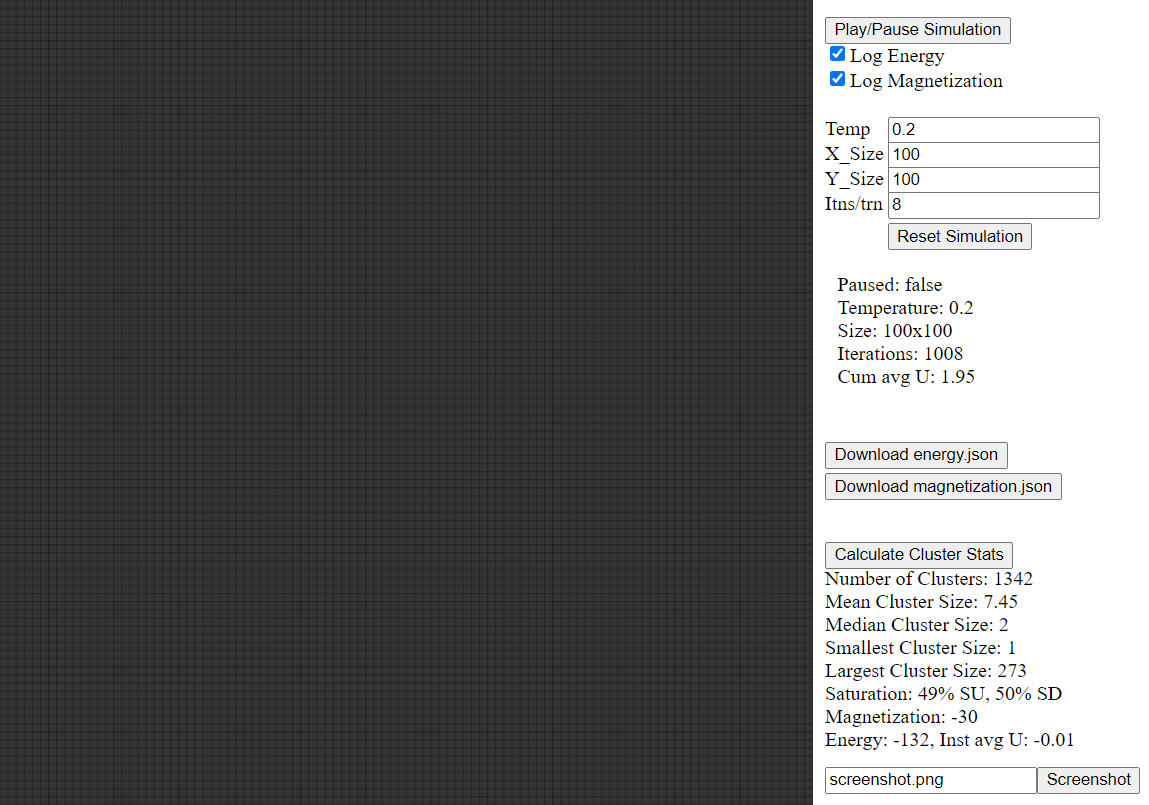Ising Model Simulation with lattice size of 100x100. Simulation converges quickly due to small temperature value of 0.2.
Implementation
My implementation of this model uses the p5.js JavaScript framework and native HTML elements to provide an interactive web interface which allows the user to manipulate parameters in real time.
In this approximation of a real lattice system, I used periodic boundary conditions. This allows us to neglect edge effects by emulating an infinite lattice. I also simplified the problem to two dimensions for simplicity.
In addition to the primary Ising Model algorithm, I developed a “cluster searching” algorithm that searches the lattice for contiguous “clusters” of like-aligned dipoles. With this information, it is able to calculate some basic statistics about the size and number of clusters, which is highly insightful for analyzing critical parameters that lead to convergence.
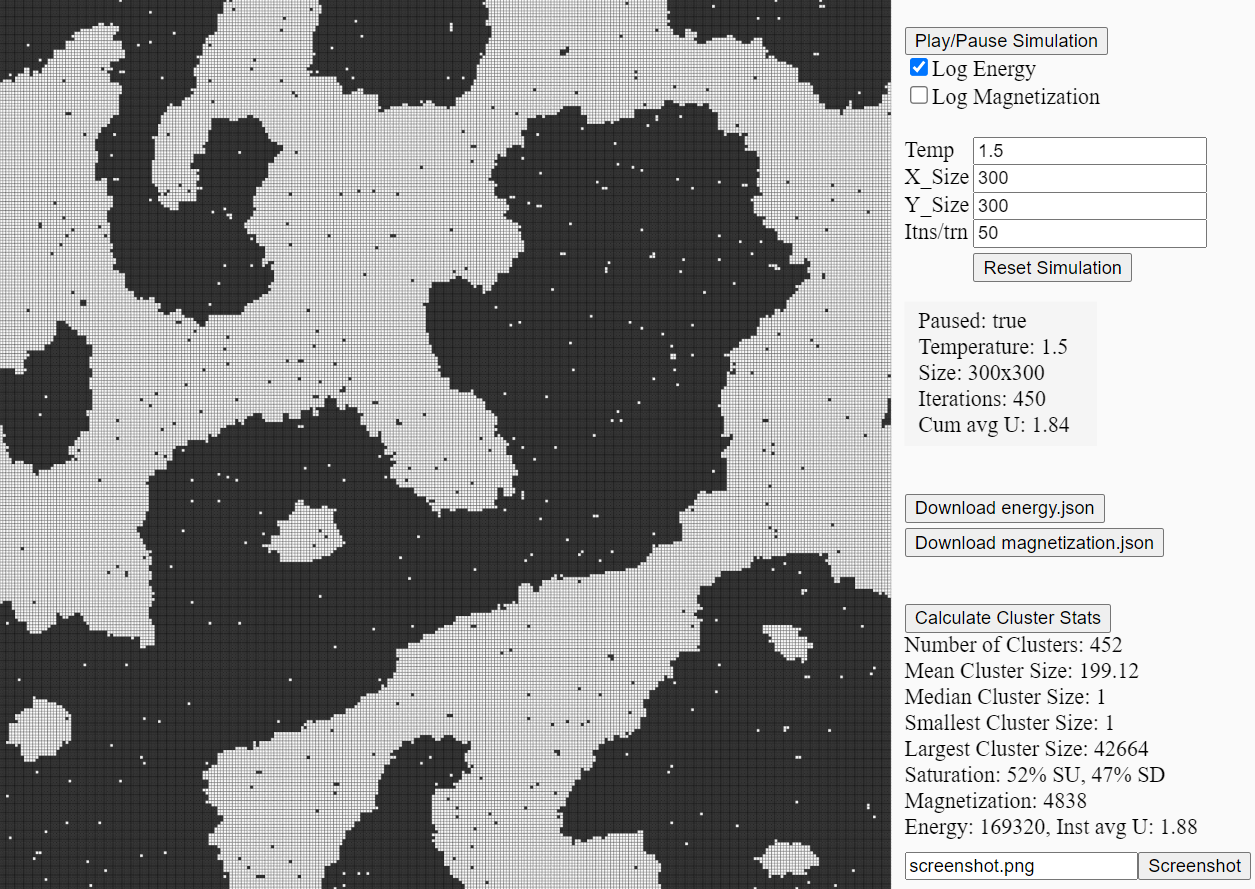Ising Model Simulation interactive web interface running with a lattice size of 300x300 after 450 iterations.
This work is inspired by the Chapter 8 problems and pseudocode in An Introduction to Thermal Physics by Daniel V. Schroeder, and was completed for a class final project in Physics 120, Thermal Physics.